libfranka
Before continuing with this chapter, please install or compile libfranka for Linux.
API documentation for the latest version of libfranka is available at
https://frankaemika.github.io/libfranka.
Libfranka changelog is available at CHANGELOG.md.

Schematic overview
libfranka is the C++ implementation of the client side of the FCI. It handles the network
communication with Control and provides interfaces to easily:
execute non-realtime commands to control the Hand and configure Arm parameters.
execute realtime commands to run your own 1 kHz control loops.
read the robot state to get sensor data at 1 kHz.
access the model library to compute your desired kinematic and dynamic parameters.
During operation you might also encounter several errors that we detail at the end of this section.
Non-realtime commands
Non-realtime commands are blocking, TCP/IP-based and always executed outside of any realtime control loop. They encompass all of the Hand commands and some configuration-related commands for the Arm.
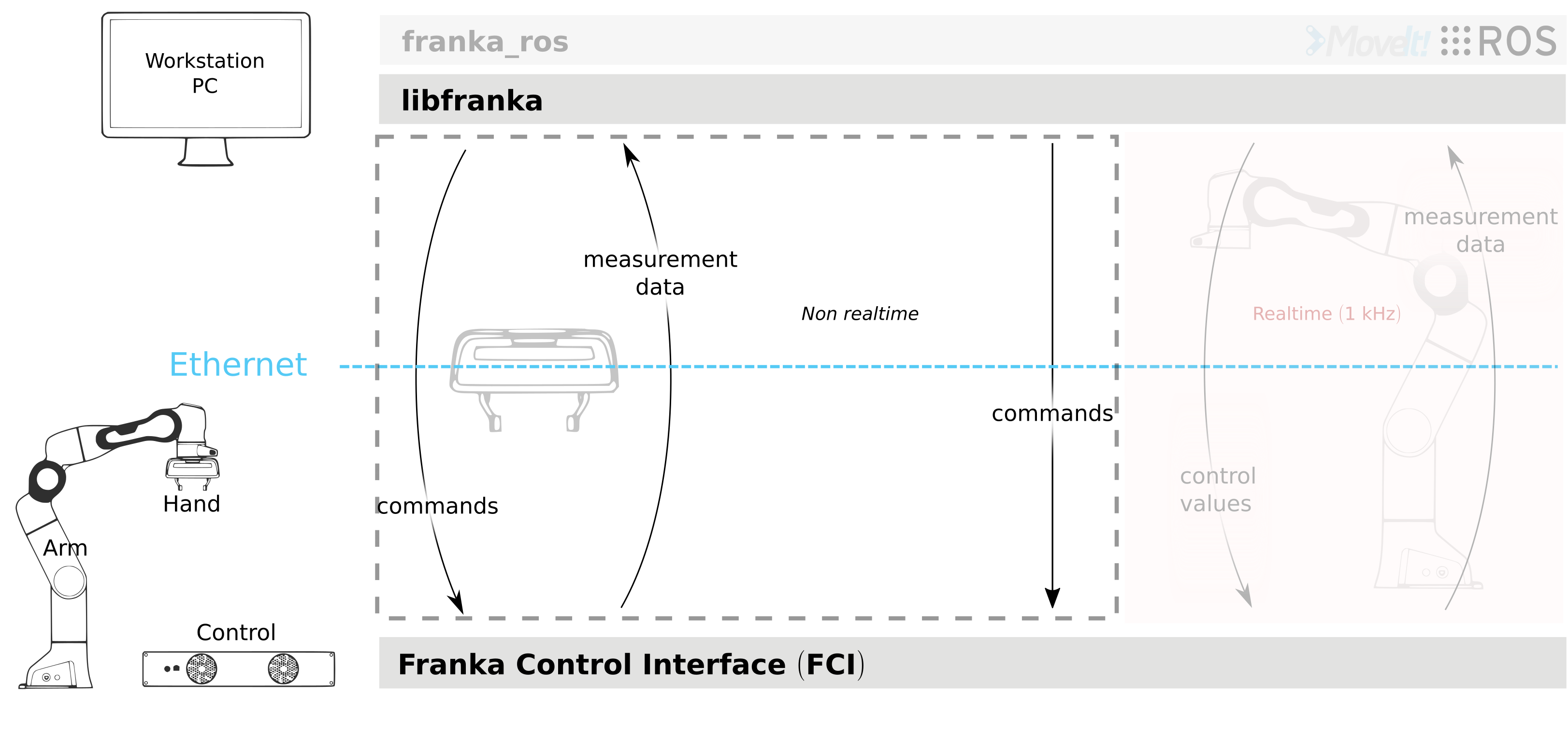
Non-realtime commands for both Arm and Hand.
The most relevant ones for the Hand are
homingwhich calibrates the maximum grasping width of the Hand.
move,graspandstop, to move or grasp with the Hand.
readOnce, which reads the Hand state.
Concerning the Arm, some useful non-realtime commands are:
setCollisionBehaviorwhich sets the contact and collision detection thresholds.
setCartesianImpedanceandsetJointImpedancewhich set the impedance parameters for the internal Cartesian impedance and internal joint impedance controllers.
setEEsets the transformation NE_T_EE from nominal end effector to end effector frame. The transformation from flange to end effector frame F_T_EE is split into two transformations: F_T_NE and NE_T_EE. The transformation from flange to nominal end effector frame F_T_NE can only be set through the administrator’s interface.
setKsets the transformation EE_T_K from end effector frame to stiffness frame.
setLoadsets the dynamic parameters of a payload.
automaticErrorRecoverythat clears any command or control exception that previously happened in the robot.
For a complete and fully specified list check the API documentation for the Robot or the Gripper.
All operations (non-realtime or realtime) on the Arm or the Hand are performed through the
franka::Robot and franka::Gripper objects respectively. A connection to the Arm/Hand
will be established when the object is created:
#include <franka/robot.h>
#include <franka/gripper.h>
...
franka::Gripper gripper("<fci-ip>");
franka::Robot robot("<fci-ip>");
The address can be passed either as a hostname or an IP address. In case of any error, either due
to networking or conflicting library version, an exception of type franka::Exception will
be thrown. When using several robots at the same time, simply create several objects with
appropriate IP addresses.
To run a specific command, simply call the corresponding method, e.g.
gripper.homing();
robot.automaticErrorRecovery();
Realtime commands
Realtime commands are UDP based and require a 1 kHz connection to Control. There are two types of realtime interfaces:
Motion generators, which define a robot motion in joint or Cartesian space.
Controllers, which define the torques to be sent to the robot joints.
There are 4 different types of external motion generators and 3 different types of controllers (one external and 2 internal) as depicted in the following figure:
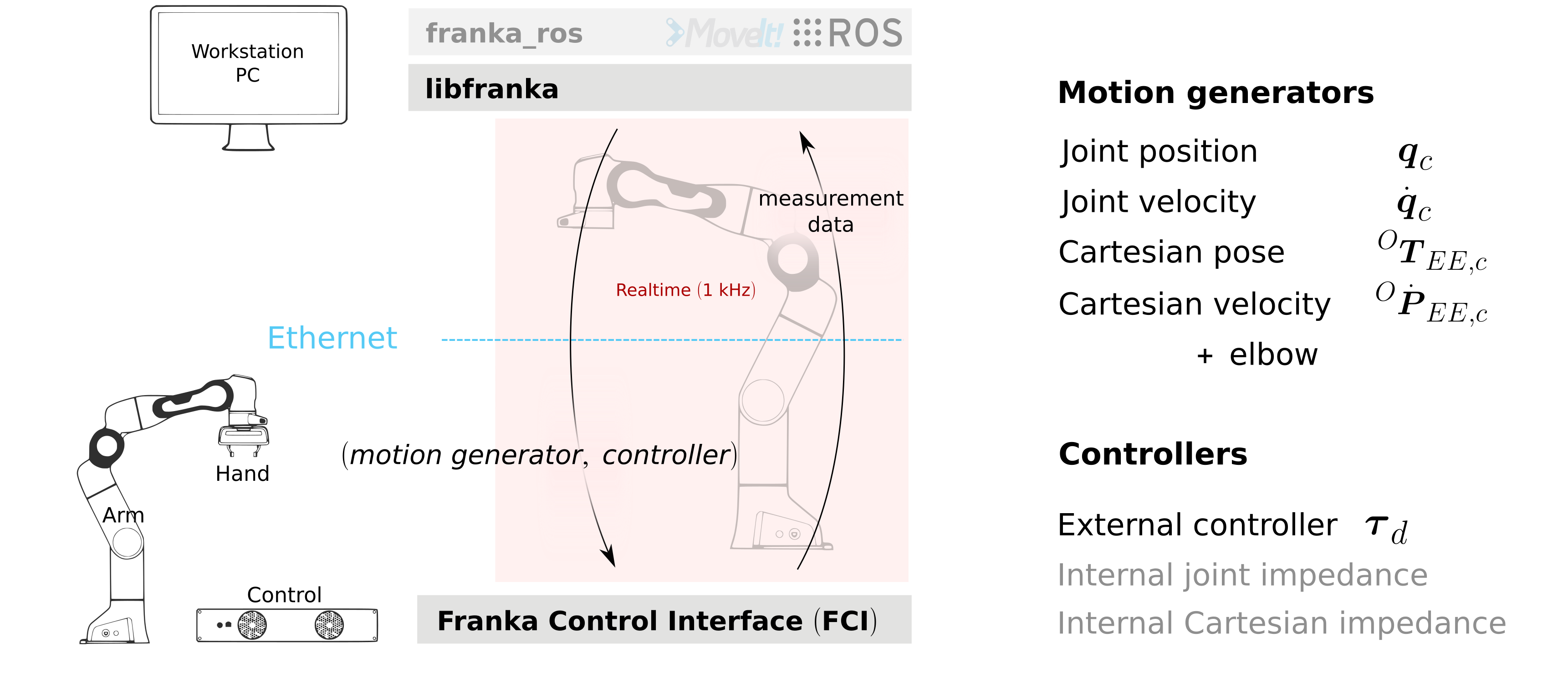
Realtime interfaces: motion generators and controllers.
You can either use a single interface or combine two different types. Specifically, you can command:
only a motion generator and therefore use one of the two internal controllers to follow the commanded motion.
only an external controller and ignore any motion generator signals, i.e. torque control only.
a motion generator and an external controller to use the inverse kinematics of Control in your external controller.
All realtime loops (motion generator or controller) are defined by a callback function that
receives the robot state and the duration of the last cycle (1 ms unless packet losses occur)
and returns the specific type of the interface. The control method of the franka::Robot
class will then run the control loop by executing the callback function at a 1 kHz frequency,
as shown in this example
std::function<franka::Torques(const franka::RobotState&, franka::Duration)>
my_external_controller_callback;
// Define my_external_controller_callback
...
std::function<franka::JointVelocities(const franka::RobotState&, franka::Duration)>
my_external_motion_generator_callback;
// Define my_external_motion_generator_callback
...
try {
franka::Robot robot("<fci-ip>");
// only a motion generator
robot.control(my_external_motion_generator_callback);
// only an external controller
robot.control(my_external_controller_callback);
// a motion generator and an external controller
robot.control(my_external_motion_generator_callback, my_external_controller_callback);
} catch (franka::Exception const& e) {
std::cout << e.what() << std::endl;
return -1;
}
return 0;
}
All control loops are finished once the motion_finished flag of a realtime command is set
to true. An excerpt of the generate_joint_velocity_motion example included
in the libfranka examples is shown here
robot.control(
[=, &time](const franka::RobotState&, franka::Duration period) -> franka::JointVelocities {
time += period.toSec();
double cycle = std::floor(std::pow(-1.0, (time - std::fmod(time, time_max)) / time_max));
double omega = cycle * omega_max / 2.0 * (1.0 - std::cos(2.0 * M_PI / time_max * time));
franka::JointVelocities velocities = {{0.0, 0.0, 0.0, omega, omega, omega, omega}};
if (time >= 2 * time_max) {
std::cout << std::endl << "Finished motion, shutting down example" << std::endl;
return franka::MotionFinished(velocities);
}
return velocities;
});
In this case, the callback function is defined directly in the call of the
robot.control( ... ) function. It uses the joint velocity motion generator interface,
as it returns a franka::JointVelocities object. It commands joint velocities to the last four
joints and move them by approx. +/-12 degrees. After 2 * time_max seconds it will return a
motion_finished flag by setting it to true with the franka::MotionFinished method and
the control loop will stop.
Note that if you use only a motion generator, the default controller is the internal joint impedance controller. You can however use the internal Cartesian impedance controller by setting the optional argument of the control function, e.g.
// Set joint impedance (optional)
robot.setJointImpedance({{3000, 3000, 3000, 3000, 3000, 3000, 3000}});
// Runs my_external_motion_generator_callback with the default joint impedance controller
robot.control(my_external_motion_generator_callback);
// Identical to the previous line (default franka::ControllerMode::kJointImpedance)
robot.control(my_external_motion_generator_callback, franka::ControllerMode::kJointImpedance);
// Set Cartesian impedance (optional)
robot.setCartesianImpedance({{2000, 2000, 2000, 100, 100, 100}});
// Runs my_external_motion_generator_callback with the Cartesian impedance controller
robot.control(my_external_motion_generator_callback, franka::ControllerMode::kCartesianImpedance);
For writing a controller, the franka::Robot::control function is used as well. The following
example shows a simple controller commanding zero torque for each joint. Gravity is
compensated by the robot.
robot.control([&](const franka::RobotState&, franka::Duration) -> franka::Torques {
return {{0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0}};
});
You can find examples for all interfaces and combinations of control loops in the
examples. Prior to running
the examples, verify that the robot has enough free space to move without colliding. Then, for
instance for the generate_joint_velocity_motion example execute the following command from
the libfranka build directory:
./examples/generate_joint_velocity_motion <fci-ip>
Warning
For writing your own motion generators or controllers it is crucial to deliver a smooth signal to the robot. Nonsmooth signals can easily generate discontinuity errors or even make the robot unstable. Check the interface specifications before starting.
Signal processing
To facilitate the control of the robot under non-ideal network connections, libfranka includes signal processing functions that will modify the user-commanded values to make them conform with the limits of the interface. There are two optional functions included in all realtime control loops:
A first-order low-pass filter to smooth the user-commanded signal.
A rate limiter, that saturates the time derivatives of the user-commanded values.
As of version
0.5.0, libfranka includes a low-pass filter for all realtime interfaces running by default with a 100 Hz cutoff frequency. The filter smooths commanded signals to provide more stable robot motions but does not prevent the violation of the limits of the interface.As of version
0.4.0, rate limiters for all realtime interfaces are running by default. Rate limiters, also called safe controllers, will limit the rate of change of the signals sent by the user to prevent the violation of the limits of the interface. For motion generators, it will limit the acceleration and jerk, while, for an external controller, it will limit the torque rate. Their main purpose is to increase the robustness of your control loop. In case of packet losses, even when the signals that you send conform with the interface limits, Control might detect a violation of velocity, acceleration or jerk limits. Rate limiting will adapt your commands to make sure that this does not happen. Check the noncompliant errors section for more details.Caution
Rate limiting will ensure no limits are violated except for the joint limits after inverse kinematics, whose violation produces the family of errors starting with
cartesian_motion_generator_joint_*. Check the noncompliant errors section for more details.Hint
The limits used in the rate limiter are defined in
franka/rate_limiting.hand are set to the interface limits. If this produces a jerky or unstable behavior you can set the limits to lower values, activate the low-pass filter or reduce its cutoff frequency.
To control the signal processing functions, all robot.control() function calls
have two additional optional parameters. The first one is a flag to activate or
deactivate the rate limiter while the second one
specifies the cutoff frequency of the first-order low-pass filter. If the cutoff frequency
>=1000.0 the filter will be deactivated. For instance
// Set Cartesian impedance (optional)
robot.setCartesianImpedance({{2000, 2000, 2000, 100, 100, 100}});
// Runs my_external_motion_generator_callback with the Cartesian impedance controller,
// rate limiters on and low-pass filter with 100 Hz cutoff
robot.control(my_external_motion_generator_callback, franka::ControllerMode::kCartesianImpedance);
// Identical to the previous line (default true, 100.0 Hz cutoff)
robot.control(my_external_motion_generator_callback, franka::ControllerMode::kCartesianImpedance, true, 100.0);
// Runs my_external_motion_generator_callback with the Cartesian impedance controller,
// rate limiters off and low-pass filter off
robot.control(my_external_motion_generator_callback, franka::ControllerMode::kCartesianImpedance, false, 1000.0);
Or similarly for an external controller
// With rate limiting and filter
robot.control(my_external_controller);
// Identical to the previous line (default true, 100.0 Hz cutoff)
robot.control(my_external_controller, true, 100.0);
// Without rate limiting but with low-pass filter (100.0 Hz)
robot.control(my_external_controller, false);
// Without rate limiting and without low-pass filter
robot.control(my_external_controller, false, 1000.0);
Danger
The low-pass filter and the rate limiter are robustness features against packet losses
to be used after you have already designed a smooth motion generator or controller.
For the first tests of a new control loop we strongly recommend to deactivate these
features.
Filtering and limiting the rate of a nonsmooth signal can yield instabilities or
unexpected behavior. Too many packet losses can also generate unstable behavior.
Check your communication quality by monitoring the control_command_success_rate
signal of the robot state.
Under the hood
Until now we have covered details of the interface running on the client side, i.e your own workstation PC. The behavior of the full control loop including the Control side of the realtime interface is shown in the following figure
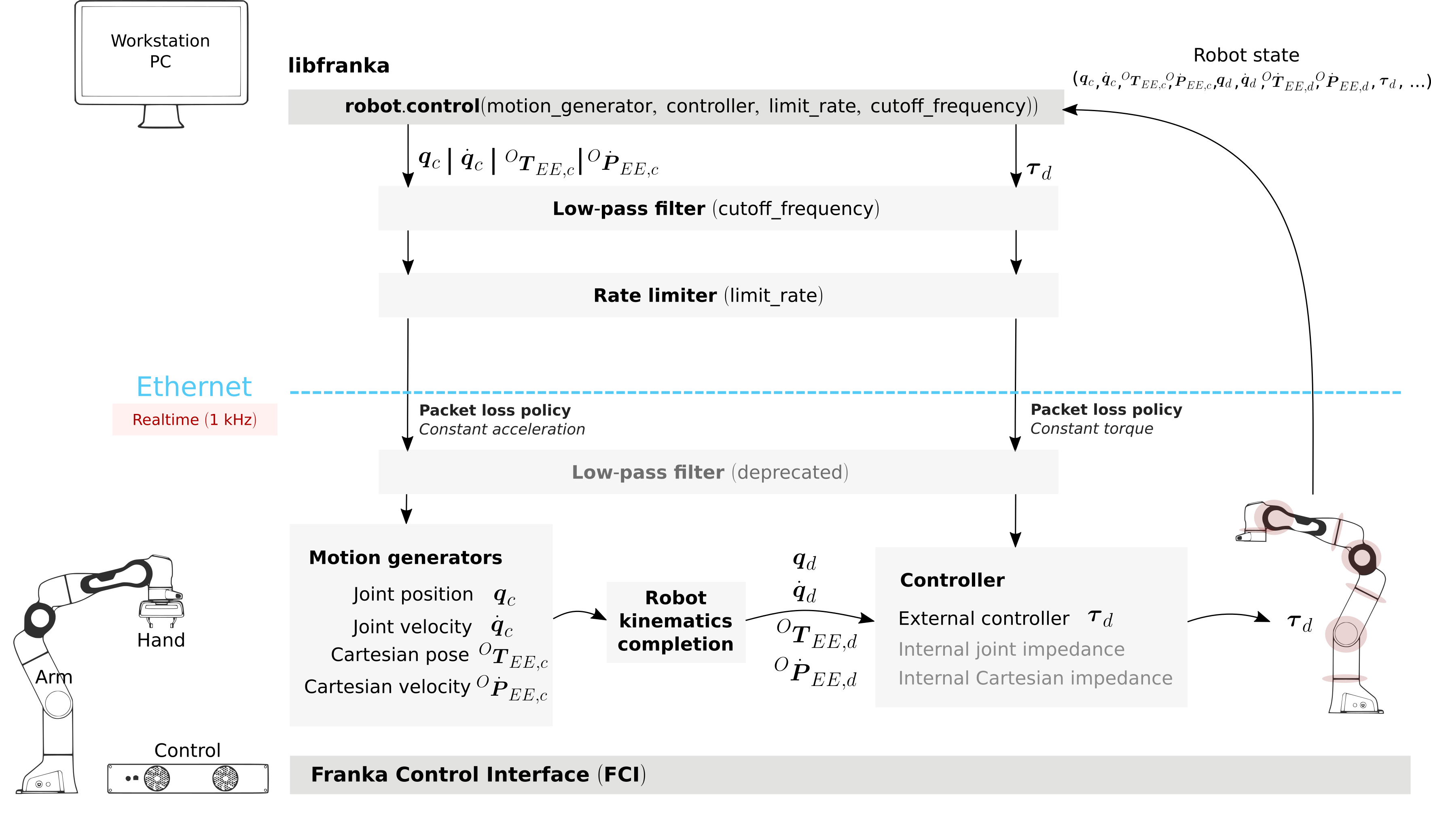
Realtime loop: from control commands to the robot desired joint torques.
Motion generators: all motion generator commands sent by the user have the subscript c
which stands for ‘commanded’. When a motion generator is sent, the Robot Kinematics completion
block will compute the forward/inverse kinematics of the user-commanded signal yielding the
‘desired’ signals, subscript d. If an internal controller is used, it will generate the
necessary torques
Hint
When you are using a joint motion generator, the Robot kinematics completion block will
not modify the commanded joint values and therefore
External controller: if an external controller is sent, the desired joint torques commanded
by the user
Where:
Note that, on the Control side, there are two things that could modify your signals:
Packet losses, which may occur if you:
don’t have a very good connection due to the performance of your PC + network card.
your control loop is taking too long to compute (you have, depending on you network card and PC configuration, approx. < 300
In this case, Control assumes a constant acceleration model or a constant torque to extrapolate your signals. If
>=20packets are lost in a row the control loop is stopped with thecommunication_constraints_violationexception.
Hint
If you are not sure if your signals are being filtered or extrapolated, you can always check the
last commanded values that you sent and compare them with the values you receive on the robot
state in the next sample. You will also find these values after an exception occurs in the
franka::ControlException::log member of the exception.
Robot state
The robot state delivers the robot sensor readings and estimated values at a 1 kHz rate. It provides:
Joint level signals: motor and estimated joint angles and their derivatives, joint torque and derivatives, estimated external torque, joint collision/contacts.
Cartesian level signals: Cartesian pose, configured endeffector and load parameters, external wrench acting on the endeffector, Cartesian collision
Interface signals: the last commanded and desired values and their derivatives, as explained in the previous subsection.
For a complete list check the API of the franka::RobotState
RobotState.
As shown in the the previous subsection, the robot state is always an input of all callback
functions for control loops. However, if you wish to only read the robot state without controlling
it, the functions read or readOnce can be used to gather it, e.g. for
logging or visualization purposes.
With a valid connection, a single sample of the robot state can be read using the readOnce
function:
franka::RobotState state = robot.readOnce();
The next example shows how to continuously read the robot state using the read function and a
callback. Returning false in the callback stops the loop. In the following, an excerpt of the
echo_robot_state example is shown:
size_t count = 0;
robot.read([&count](const franka::RobotState& robot_state) {
// Printing to std::cout adds a delay. This is acceptable for a read loop such as this,
// but should not be done in a control loop.
std::cout << robot_state << std::endl;
return count++ < 100;
});
Model library
The robot model library provides
The forward kinematics of all robot joints.
The body and zero jacobian matrices of all robot joints.
Dynamic parameters: inertia matrix, Coriolis and centrifugal vector and gravity vector.
Note that after you load the model library, you can compute kinematic and dynamic parameters for an arbitrary robot state, not just the current one. You can also use the model library in a non realtime fashion, e.g. in an optimization loop. The libfranka examples include exemplary code for printing joint poses or computing jacobians.
Errors
Using the FCI you will encounter several errors that happen either due to noncompliant commands sent by the user, due to communication problems or due to the robot behavior. The most relevant ones are detailed in the following subsections. For a complete list please check the API documentation at Errors.
Hint
Note that, after an error occurs, you can automatically clear it and continue running your
program with the franka::Robot::automaticErrorRecovery() command without user intervention.
Check the exception string before continuing to make sure that the error is not a critical
one.
Some errors can also be cleared manually by toggling the external activation device or by using the error recovery button in Desk.
Errors due to noncompliant commanded values
If the commanded values sent by the user do not comply with the interface requirements, one of the following errors will occur:
Errors due to wrong initial values of a motion generator:
joint_motion_generator_start_pose_invalid
cartesian_position_motion_generator_start_pose_invalid
cartesian_motion_generator_start_elbow_invalid
cartesian_motion_generator_elbow_sign_inconsistentThese errors indicate a discrepancy between the current robot values and the initial values sent by the user. To fix these errors, make sure that your control loop starts with the last commanded value observed in the robot state. For instance, for the joint position interface
double time{0.0}; robot.control( [=, &time](const franka::RobotState& robot_state, franka::Duration period) -> franka::JointPositions { time += period.toSec(); if (time == 0) { // Send the last commanded q_c as the initial value return franka::JointPositions(robot_state.q_c); } else { // The rest of your control loop ... } });
Errors due to a position limit violation using a joint position/velocity motion generator, which will produce a
joint_motion_generator_position_limits_violation. Solving this error should be simple: make sure that the values that you send are in the limits. Cartesian interfaces also have limits on the joint signals that result after the inverse kinematics: thecartesian_motion_generator_joint_position_limits_violationwill be triggered if the inverse kinematics solver of Control yields a joint configuration out of the limits.Errors due to velocity limits violation and discontinuity errors, which refer to acceleration and/or jerk limits violation. If you use a joint motion generator the possible errors are
joint_motion_generator_velocity_limits_violation
joint_motion_generator_velocity_discontinuity(acceleration limit violation)
joint_motion_generator_acceleration_discontinuity(jerk limit violation)If you use a Cartesian one, the possible errors are
Cartesian limits:
cartesian_motion_generator_velocity_limits_violation
cartesian_motion_generator_velocity_discontinuity(acceleration limit violation)
cartesian_motion_generator_acceleration_discontinuity(jerk limit violation)Joint limits after the inverse kinematics
cartesian_motion_generator_joint_velocity_limits_violation
cartesian_motion_generator_joint_velocity_discontinuity(acceleration limit violation)
cartesian_motion_generator_joint_acceleration_discontinuity(jerk limit violation)To mitigate velocity violations or discontinuity errors, make sure that the signals that you command do not violate the limits. For every motion generator, Control differentiates the signals sent by the user with backwards Euler. For instance, if, using a joint position motion generator, at time
the user sends the command , the resulting velocity, acceleration and jerk will be
Velocity
Acceleration
Jerk
, where
. Note that and are always sent back to the user in the robot state as and so you will be able to compute the resulting derivatives in advance, even in case of packet losses. Check the section about the details of the Control side of the interface for more details. Finally, for the torque interface a torque rate limit violation triggers the error
controller_torque_discontinuityControl also computes the torque rate with backwards Euler, i.e.
. The previous desired torque commanded by the user is also sent back in the robot state as so you will also be able to compute the resulting torque rate in advance, even in case of packet losses.
Hint
The rate limiters included in libfranka since version 0.4.0 modify the signals
sent by the user to make them conform with all these limits except for the joint limits
after the inverse kinematics. You can check the include/franka/rate_limiting.h and
src/rate_limiting.cpp for exemplary code on how to compute resulting velocity,
acceleration and jerk for all interfaces. We emphasize again that using rate limiting on a
discontinuous signal can easily yield to unstable behavior, so please make sure that
your signal is smooth enough before enabling this robustness feature.
Errors due to communication problems
If during a realtime loop Control does not receive any packets during 20 cycles, i.e. 20 ms, you
will receive a communication_constraints_violation error.
Note that if your connection has intermittent packet drops, it might not stop, but it could
trigger discontinuity errors even when your source signals conform with the interface
specification.
In that case, check our troubleshooting section
and consider enabling the signal processing functions
to increase the robustness of your control loop.
Behavioral errors
Warning
These monitoring features are by no means conform with any safety norm and do not guarantee any safety to the user. They only aim for helping researchers during the development and testing of their control algorithms.
Reflex errors. If the estimated external torques
cartesian_reflexorjoint_reflexerror will be triggered respectively. You can configure the thresholds with thefranka::Robot::setCollisionBehaviornon realtime command.Hint
If you wish the robot to have contacts with the environment you must set the collision thresholds to higher values. Otherwise, once you grasp an object or push against a surface, a reflex will be triggered. Also, very fast or abrupt motions without contacts could trigger a reflex if thresholds are low; the external torques and forces are only estimated values that could be innacurate depending on the robot configuration, especially during high acceleration phases. You can monitor their values observing
Self-collision avoidance. If the robot reaches a configuration which is close to a self-collision, it will trigger a
self_collision_avoidance_violationerror.Warning
This error does not guarantee that the robot will prevent a self collision at any configuration and speed. If, using the torque interface, you drive the robot at full speed against itself the robot might self-collide.
If the torque sensor limit is reached, a
tau_j_range_violationwill be triggered. This does not guarantee that the sensor will not be damaged after any high-torque interactions or motions but aims for preventing some of it.If the maximum allowed power is reached, the
power_limit_violationwill be triggered. It will prevent the robot from moving and continuing the control loop.If you reach the joint or the Cartesian limits you will get a
joint_velocity_violationor acartesian_velocity_violationerror respectively.